A while back I was in a situation where I had to teach evolution to some grade nine students. I am more of the physical science/math teacher, and biology is not my cup of tea.
In physics, there are also unproven “theories” that we follow. In fact, all of Newtonian physics is pretty much “false” and yet we teach it all the time as fundamental physics. Light is both a wave and a particle… how can that ever be possible? Either it can travel through objects (like a wave / energy) or it is stopped by objects (like a particle)? For some reason, the physical theories don’t affect people in the same emotional way as the theory of evolution. We have a way of dealing with the physics theories on a logic / thinking level. No religion is offended (although ~400 years ago, Copernicus’ theory of planetary motion around the sun was dissputed by the Catholic church). Nobody’s extreme beliefs come under fire with all these silly physics theories.
But not the same can be said about the theory of evolution. In a group of 25 students, there is always bound to be at least one student hating the teacher when evolution is being discussed. Their parents at home teach them something, and then their biology teacher is teaching something completely opposite. The nerve of the teacher to contradict their belief system!
As a scientist, I am of course an evolutionary theory proponent, but I realized that in this particular group of students, there were a few “non-evolutionary” believers. I found it hard to teach them even the basic ideas of evolution without constantly having to debate the subject. These kids were really smart and prepared, and new how to argue the point better than I could. I really had a hard time getting through a lesson without interuption. As a teacher I realize that even though debating is great, time during class runs out fast, yet the curriculum has to be covered, and WE NEED TO MOVE ON>>>.
I did want to teach the theory of natural selection to these particular grade nine students and of course all the other students in the class. I also wanted to do it so that I wasn’t just lecturing them on the concept, telling them: “Believe me, I am your all knowing teacher, I have all the answers. Don’t believe your parents, they don’t know what they’re talking about…” With such a touchy subject, I had to get really really creative!
So, with the help of my computer scientist husband, I invented a game to show the students how computer scientists use “evolution” to solve very complex problems (in computer science lingo this is called: Genetic Algorithms). In such a case, there was no reason to get all upset about the “evil evolution”. I was not attacking the students’ personal beliefs. I was just explaining it as a set of game rules – more like physical set of principals – that ultimately allow for the best possible outcome. If the students chose to believe that this is actually what happens when going from one species to another, like in the Darwinian theory of evolution, was their choice. But I could at least teach the students the jist of the theory, without having the huge debate.
Here it is my game:
The Genetic Algorithm Game – Solving a Complex Pathway Problem with Evolution:
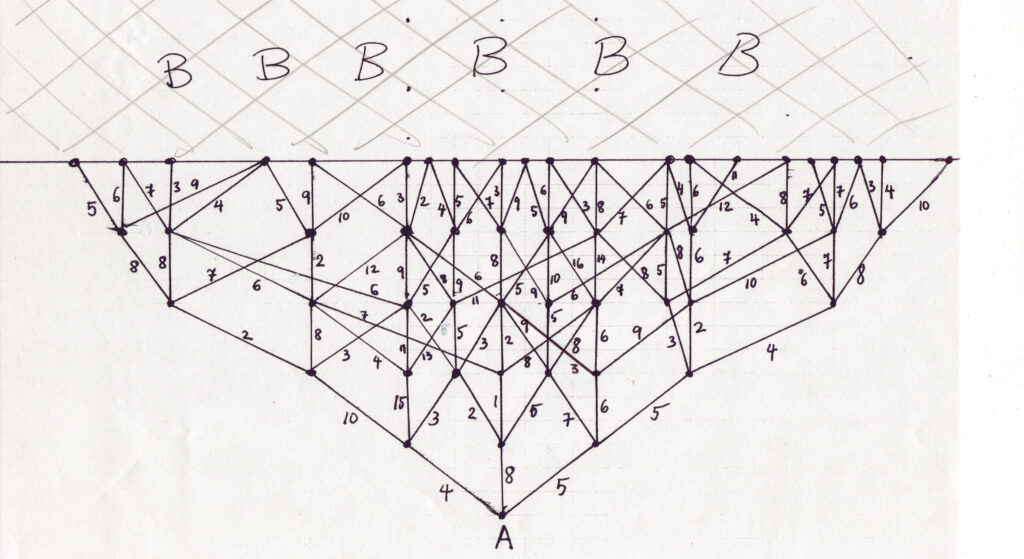
You start with a complex map (see the picture above or create your own map). There is a way of getting from point A to area B in very many different combinations. Figuring out the fastest way to get there is the object of the game.
There are five sections (decisions) to the path. Starting at point A, once could go left (L), straight (S), or right (R). Each time you reach the next point (crossroads) you can choose to go left, straigt, or right. Since the path has five such points, the “genetic code” will consist of five such decisions.
For example, one student in the class can go first left, then right, then left, then straight, and finally straight to reach the final destination of B. For this student, the genetic code would be: LRLSS.
In order for the genetic code to be random, what I did with my students was make them place the three letters (L, R, S) in an envelope and then choose randomly five times to get the code. Whatever the way you get the students to choose their initial genetic code doesn’t matter, as long as they understand that it has to be random. (Initial conditions in the theory of natural selection are supposed to be random. Only after several generations of mating and mutations does the best species evolve.)
Each segment of the pathway has a number associated with it. You can make up an explanation for the number, such as distance, or time it takes to get to the next point. Whatever the reason, the lower number is what’s best for our purposes. The sum of all the segments will add up to the total number of getting from point A to area B. If we want to get from point A to area B in the shortest amount of time, the pathway with the smallest number is the best.
For the example above, the student that chose the LRLSS genetic code, his time to get to the other side would be: 4+3+2+9+3=21.
After all the students in the class have randomly selected their genetic code, have them tally up the time it took them to get from A to B. One by one, ask the students to give you their time, and record these numbers on the board.
After seeing all the numbers on the board, tell them that the students who didn’t make it under a certain time died (making up a story, that they didn’t get to the food (area B) fast enough before all of it was gone). Make sure you kill off about 1/3 of the students – these students will be the offspring of the remainder of the students in the class.
The killed off students have to get out of their seats and go to the front of the class.
Next, students in the remainder of the class have to get together with a partner (also random choice) and mate. Mating in our game means to choose a random genetic recombination of the two original pathways.
For example, if our student from the above example with genetic code LRLSS mates with another student with a code of RRLSL, the result can be anything that is some sort of combination of the original two codes. For instance it could be RRLSS, or LRLSL or any other one that comes from the previous two.
The recombination of DNA has to be done again randomly to immitate the real natural selection theory, and the way we understand genetics. This new code will be given to one of the students at the front of the class. They are the offspring of this mating.
The child then has to tally up their “time” to get from A to B and these new times have to be once again collected by you the teacher and written up on the board. Once again another threshold is chosen (a number where some students are “killed off” and sent to the front of the class to await getting reborn).
This continues for a few generation. Each time, there should be an apparent improvement in the time. After a few matings, the time should get faster and faster to get from A to B.
Once in a while, while this mating simulation is going on, you (the teacher) should impose random mutations to the genetic code. Explain this to the students that as the mating occurs, there is some gamma rays that enter the earth and change the DNA of the offspring. Or that there was a problem with the replication of DNA. Or that the sun’s infrared radiation changed the genetic code of the father.
To do this, you should go and literally change the genetic code of some of the students. Don’t do this too often, as genetic mutations don’t occur that often.
For instance, if the offspring has a genetic code of LRLSL, make him change the first letter to R.
At the end of the class, the students understand that the object of the game (figuring out the best path from A to B) is obtained. Hopefully they also see how the system of natural selection works, and how it is a very plausible theory.
A few things to mention:
- It was possible to find the best path originally, in the very first go, but that the best path will ultimately come up, with enough generations, even if it was not chosen initially.
- The genetic algorithm is actually a method used by computer scientists to search through complex systems, to solve complex problems.
- This method is not very fast (it takes many generations to get to the absolute best solution – as in evolution of species itself), but if the problem is complex enough, this is the only way of going about solving it.

